向量数据库 Vector Database

近期，随着 AI 相关话题热度提升，向量数据库也出现在了更多人的视野中。

本篇文章，让你对向量数据库有一个基本的了解。

什么是向量数据库

向量数据库是专门用来存储和查询向量的数据库，其存储的向量来自于对文本、语音、图像、视频等的向量化数据。

其主要特点是能够高效地处理包含大量向量的数据集，并支持快速的相似度搜索。
与传统的关系型数据库不同，向量数据库更适合处理高维稠密向量数据，广泛应用于图像、音频、文本等领域的人工智能和机器学习任务中。
在向量数据库中，每个向量都可以看作是一个多维空间中的点，而相似度搜索则是通过测量向量之间的距离或角度来实现的。向量数据库的发展得益于硬件技术的不断提升和机器学习领域的迅速发展，具有良好的应用前景。

什么是向量

在数学中，向量（vector）是指具有大小（magnitude）和方向（direction）的量。一般来说，向量可以在一个指定的坐标系中被表示为一组有序数（有限个实数），这些实数称为向量的分量（component）。常用的表示方式是将向量写成一个列向量或行向量的形式，例如：

列向量：\(\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}\)

行向量：\(\mathbf{v} = [v_1,v_2,\cdots,v_n]\)

其中，\(v_1, v_2, \cdots, v_n\) 是向量的\(n\)个分量。除此之外，还有一些特殊的向量，如零向量、单位向量等。

在计算机科学领域，向量常常被用来表示对象的特征，例如图像、文本、音频等。将对象转换成向量形式便于进行相似度搜索、聚类等操作。向量化的方式可以通过特征提取、文本建模、深度学习等方法来实现。

处理向量数据成为了许多应用程序的核心问题。为了解决这些问题，人们设计了各种向量数据库和向量索引技术，以提供高效的相似度搜索和近邻查询功能。

向量的实际含义

向量A [0.8,0.3]，表示有一个人，这个人喜欢 0.8 强度的喜剧片，喜欢 0.3 强度的动作

向量B [0.4,0.6]，表示一部电影，这部电影是 0.4 强度的喜剧，0.6 强度的动作片

这两个向量之间的余弦相似度计算过程：
向量的余弦相似度可以表示为：\(cos\theta = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\|\|\mathbf{b}\|}\)

其中，a 和 b 分别表示要计算余弦相似度的两个向量， \(\mathbf{a} \cdot \mathbf{b}\) 表示它们的点积，$|\mathbf{a}|$ 和 $|\mathbf{b}|$ 分别表示它们的模长。

将 a = [0.8, 0.3], b = [0.4, 0.6] 代入公式计算，有：\(\mathbf{a} \cdot \mathbf{b} = 0.8 \times 0.4 + 0.3 \times 0.6 = 0.32 + 0.18 = 0.5\)

\(\begin{aligned} \|\mathbf{a}\| &= \sqrt{0.8^2 + 0.3^2} \approx 0.854 \\ \|\mathbf{b}\| &= \sqrt{0.4^2 + 0.6^2} \approx 0.721 \end{aligned}\)

将上述计算结果代入余弦相似度公式中，可得这两个向量的余弦相似度为：\(cos\theta \approx \frac{0.5}{0.854 \times 0.721} \approx 0.852\)

算出来的这个值可以表示为 这个人喜欢这部电影的程度

余弦相似度的取值范围为[-1, 1]，值越大，代表相似度越高。

除了余弦相似度，还有一些可用于评估向量相似度的度量方法：

  1. 欧氏距离（Euclidean distance）：它衡量两个点之间的直线距离，也被称为 L2 范数。它在计算上非常简单，但有时有可能不是最佳选择。

  2. 曼哈顿距离（Manhattan distance）：它衡量两个点之间的城市街区距离，也被称为 L1 范数。它类似于欧氏距离，但它更适合于某些特定的应用场景，比如在计算跨越城市街区的驾驶路线时。

  3. 闵可夫斯基距离（Minkowski distance）：它是欧氏距离和曼哈顿距离的泛化形式。在这种情况下，一个参数被引入，该参数控制欧氏距离和曼哈顿距离之间取值的倾向性。

  4. 矢量余弦相似度（Vector cosine similarity）：这种度量方式与余弦相似度非常相似，只是这里要比较的是两个向量的单位化版本。

在实践中，通常使用向量余弦相似度来衡量向量之间的相似度，以减少向量大小对相似度的影响。

什么是向量数据

向量数据是由多个数值组成的一维数组，常用于表示文本、图像、音频等非结构化数据。在向量中，每个数值代表了该向量在某个方向上的分量。例如，在二维平面上，一个点的位置可以用一个二维向量表示，其中第一个数值代表了该点在x轴上的位置，第二个数值代表了该点在y轴上的位置。

在现代数据科学和机器学习中，向量数据被广泛应用于各种任务，如相似度匹配、聚类、分类和回归。这些任务通常需要计算向量之间的距离或相似度，并且需要对向量进行检索和排序。因此，高效处理向量数据是许多数据科学和机器学习应用程序的核心问题。为了解决这些问题，人们开发了许多向量数据库和向量索引技术，以提供高效的相似度搜索和近邻查询功能。

向量如何表示图片的特征

在计算机视觉领域中，向量通常被用来表示图片的特征。这些特征向量可以通过多种方法获得，其中最常用的是卷积神经网络（Convolutional Neural Network，简称CNN）。CNN 是一类深度学习模型，它通过卷积、池化等操作对图片进行处理，最终输出一个固定大小的向量作为该图片的特征表示。

具体而言，CNN 通过一系列的卷积层和池化层对输入图片进行特征提取，并逐渐减小特征图的尺寸和数量。在最后一层卷积层之后，通常会添加若干全连接层，将卷积层输出的高维特征转换为一个固定长度的向量。这个向量被认为是该图片的“特征表示”，它能够反映出图片的语义信息，例如物体类别、颜色、纹理等特征。这样，我们就可以使用向量距离的概念来度量不同图片之间的相似性，从而支持基于内容的图片检索、聚类等应用。

向量如何表示音频

在音频处理中，向量也可以用来表示音频的特征。其中最常见的是使用 梅尔频率倒谱系数（Mel-Frequency Cepstral Coefficients，简称MFCC）来提取音频的特征向量。

MFCC 是一种基于人耳感知特性的声学特征，它模拟了人耳对不同频率声音的感受，具有很好的区分能力。MFCC 提取过程包括以下几步：

  1. 预加重：对原始音频信号进行高通滤波，增强高频部分的能量。

  2. 分帧：将音频信号分割成若干个长度相等的帧。

  3. 加窗：对每一帧应用汉明窗等窗函数，减少频谱泄漏。

  4. 傅里叶变换：对每一帧的信号进行离散傅里叶变换（DFT），得到其频域表达。

  5. 梅尔滤波器组：将频域信号通过一组梅尔滤波器，将其转换为梅尔频率域的信号。

  6. 对数压缩：对每个滤波器组输出值取对数，以便更好地表示人耳对音量的感知。

  7. 离散余弦变换：对每个滤波器组输出值进行离散余弦变换（DCT），得到其MFCC系数。

最终，MFCC 系数被组合成一个向量作为音频的特征表示。这个向量通常包含20-40个元素，每个元素代表一个MFCC系数，反映了音频中不同频率的能量分布情况。这样，我们就可以使用向量距离的概念来度量不同音频之间的相似性，从而支持基于内容的音频检索、分类等应用。

向量如何表示文本

在自然语言处理中，向量也常被用来表示文本的特征。一个常见的方法是使用词袋模型（Bag-of-Words Model）以及词向量（Word Embedding）。

词袋模型是一种基于频次的文本表示方法，它将文本表示为一个由每个单词出现次数所组成的向量。具体而言，假设我们有一个包含 \(N\) 个文档的文本集合，其中每个文档由若干个单词组成。那么词袋模型将该文本集合表示为 \(N\) 个 \(M\) 维向量的矩阵，其中第 \(i\) 个向量表示第 \(i\) 个文档中每个单词出现的次数。这样，我们就可以使用向量距离的概念来度量不同文档之间的相似性，从而支持基于内容的文本分类、聚类等应用。

词向量是一种更加高级的文本表示方法，它将每个单词映射到一个连续的向量空间中，并且使得语义上相似的单词在向量空间中彼此接近。其中最常用的词向量模型是 Word2Vec，它通过训练神经网络来学习单词的向量表示。与词袋模型不同，词向量不仅考虑了单词出现的频率，还学习了单词之间的语义关系，因此能够更好地捕捉文本的语义信息。这样，我们就可以使用向量相似度的概念来进行文本匹配、情感分析等
任务。

与传统关系型数据库的区别

与传统关系型数据库相比，向量数据库具有以下几个区别：

  1. 数据模型不同：传统关系型数据库采用表格方式存储数据，而向量数据库则采用向量方式存储数据。向量数据库中每个记录都是一个向量，而不是传统数据库中的行。

  2. 查询方式不同：传统关系型数据库通常使用SQL语言进行查询，而向量数据库则支持基于向量相似度的查询。这种查询方式能够快速地找到相似的向量数据，适用于人工智能和机器学习领域的一些任务，如推荐系统、图像搜索和自然语言处理等。

  3. 存储和索引技术不同：向量数据库采用向量化存储和索引技术，能够高效地处理包含大量向量的数据集，而传统关系型数据库则采用B树等索引结构。在向量数据库中，每个向量都可以看作是多维空间中的点，而索引则是通过测量向量之间的距离或角度来实现的。

  4. 应用场景不同：传统关系型数据库适用于业务管理和数据分析等场景，而向量数据库则更适合处理高维稠密向量数据，并广泛应用于图像、音频、文本等领域的人工智能和机器学习任务中。

向量数据库也支持 CRUD。对向量更快的相似性搜索。

向量数据库中的名词

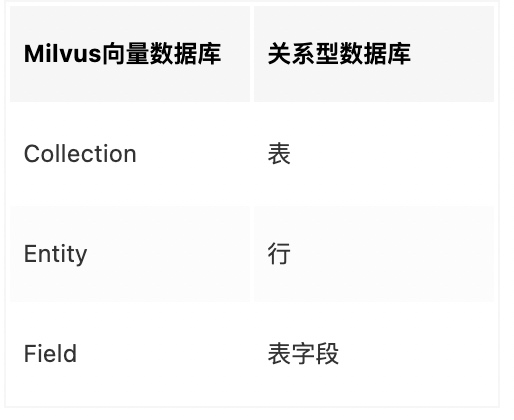
向量数据库的应用场景

向量数据库在人工智能和机器学习领域中有着广泛的应用场景，以下是一些常见的应用场景：

  1. 人脸识别：向量数据库可以存储大量人脸特征向量，并能够快速地检索相似的人脸，从而实现高效准确的人脸识别。

  2. 图像搜索：向量数据库可以将图像转化为高维特征向量，并根据相似度进行检索。这种技术被广泛应用于图像搜索引擎、商品推荐等领域。

  3. 推荐系统：向量数据库可以通过存储用户历史行为数据，并利用相似度计算来产生个性化推荐结果。这种技术被广泛应用于电商、社交网络等领域。

  4. 自然语言处理：向量数据库可以存储单词或文本片段的向量表示，并通过相似度计算来进行文本分类、情感分析等任务。

  5. 视频监控：向量数据库可以存储视频特征向量，以实现更加高效准确的视频检索和目标跟踪。

  6. AI 长期记忆：ChatGPT等 AI 产品的底层数据库大概率就是向量数据库。

AI 的长期记忆

众所周知，目前的大模型（无论是 NLP 领域的 GPT 系列还是 CV 领域的 ResNET 系列）都是预先训练 Pretrain 的大模型，有着非常明晰的训练截止日 Cut-off Date，这导致这些模型对于训练截止日之后发生的事情一无所知。

而随着向量数据库的引入，其内部存储的最新的信息向量能够极大地拓展大模型的应用边界，向量数据库可以使得大模型保持准实时性，提高大模型的适用性，并使得大模型能够动态调整。也就是说，向量数据库使得大模型的长期记忆得到了可能。

AutoGPT 等于 ChatGPT 加上向量数据库。通过向量数据库让 AutoGPT 具备了长期记忆能力，它知道之前搜的是什么，把历史全部记进去了，不然每次查询是没有上下文的。

如果将向量数据库部署在公司内部，能够协助解决目前企业界最担忧的大模型泄露隐私的问题。

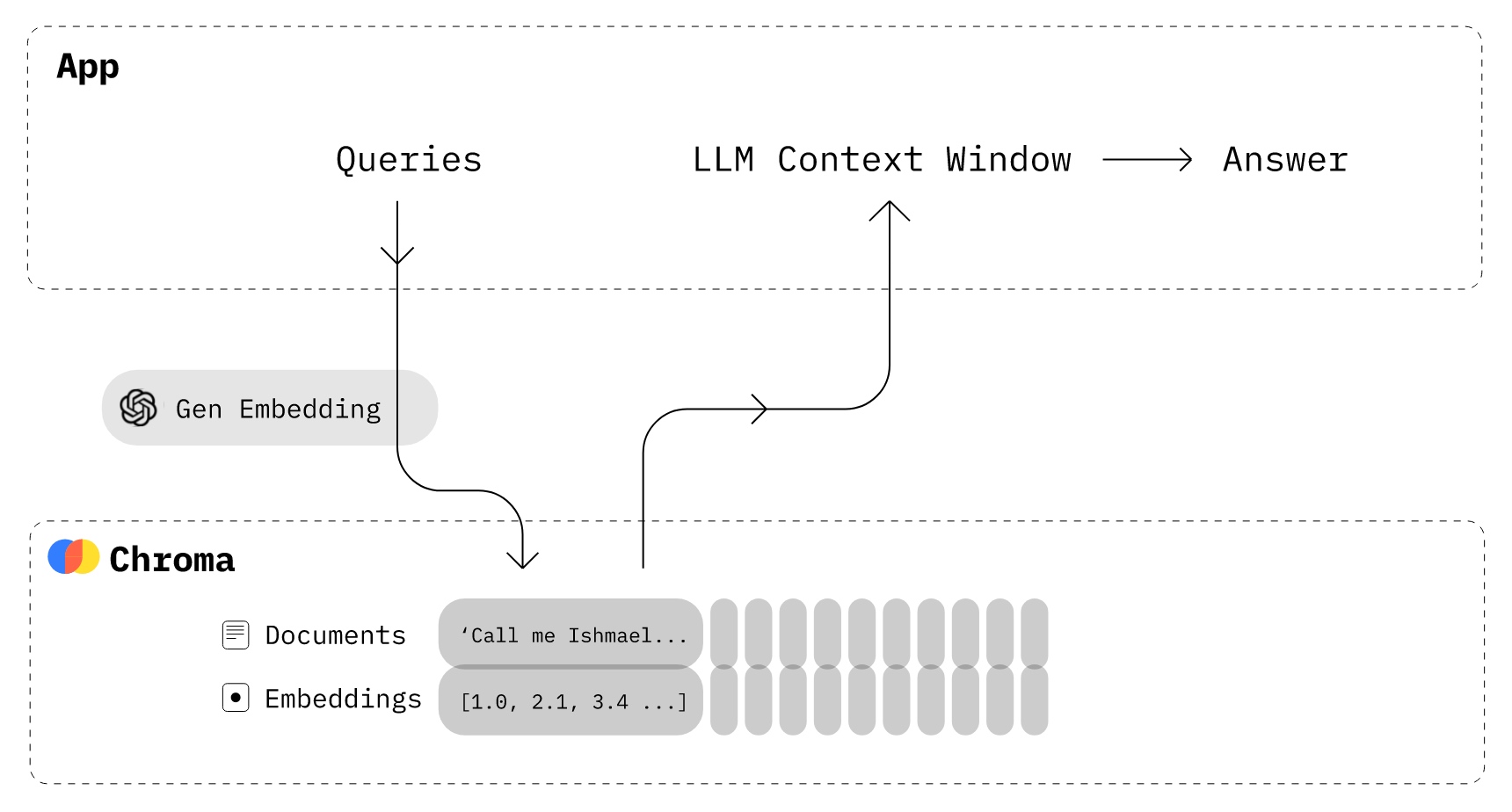
向量数据库 产品

Milvus：世界上最快的向量数据库
Pinecone，这个提供 Google Cloud 或 AWS 的托管服务，Rust 重写
Qdrant，开源版及商业版都有
pgvector，PostgreSQL 的扩展


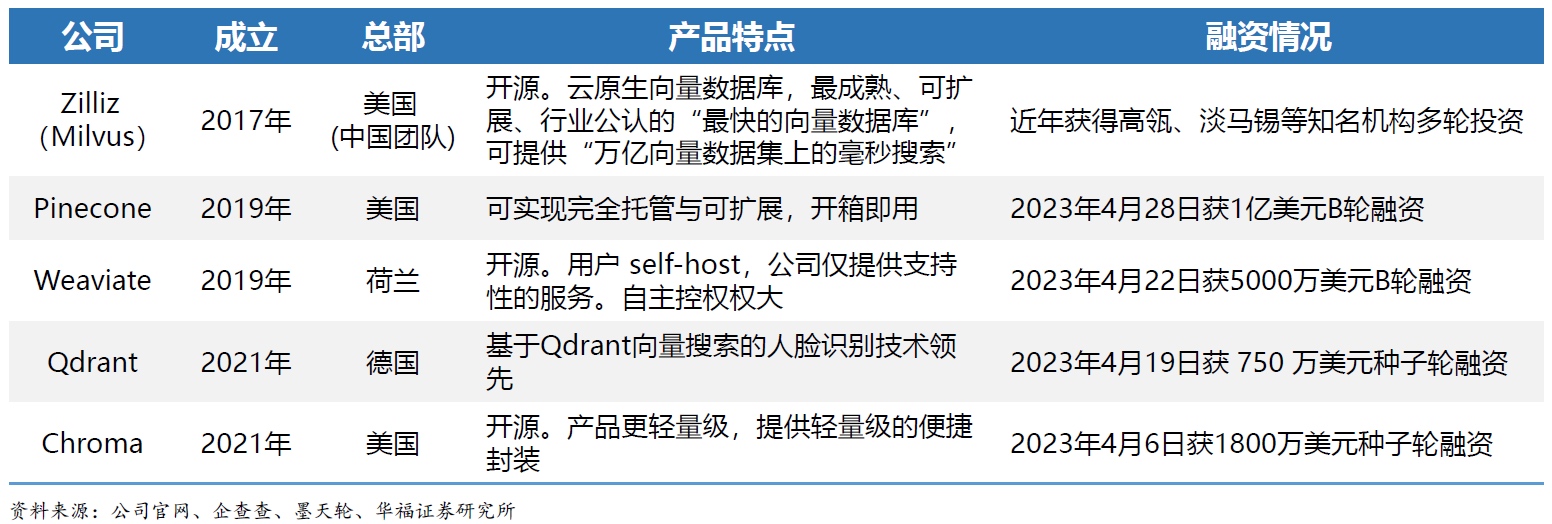
4月28日，向量数据库平台Pinecone宣布获得1亿美元（约7亿元）B轮融资，由Andreessen Horowitz领投，ICONIQ Growth等跟投。

4月22日，向量数据库平台Weaviate宣布获得5000万美元（约3.5亿元）B轮融资，由Index Ventures领投，Battery Ventures等跟投。

此外，4月6日Chroma获1800万美元种子轮融资，4月19日Qdrant获750万美元种子轮融资。

Pinecone: https://www.pinecone.io
Weaviate: https://weaviate.io
Chroma: https://www.trychroma.com/
Zilliz: https://zilliz.com
Vespa: https://vespa.ai

市场空间巨大，行业处于从0-1阶段

向量数据库是 AI 时代的 Killer App。AI时代一切AI化，而AI化的本质则是向量化，向量化计算成本高昂，海量的高维向量势必需要专门的数据库进行存储和处理，向量数据库应运而生，向量数据库在拓展AI全新应用场景的同时，也将对传统数据库产品形成替代，进而成为AI时代的Killer App。

milvus 部署：

https://github.com/milvus-io/bootcamp/tree/master/solutions/audio/audio_similarity_search/quick_deploy

Qdrant

https://qdrant.tech/documentation/overview/

docker 启动

docker run -p 6333:6333 \
    -v $(pwd)/qdrant_storage:/qdrant/storage \
    qdrant/qdrant

使用下来，感觉 Qdrant 比 millvus 好用。

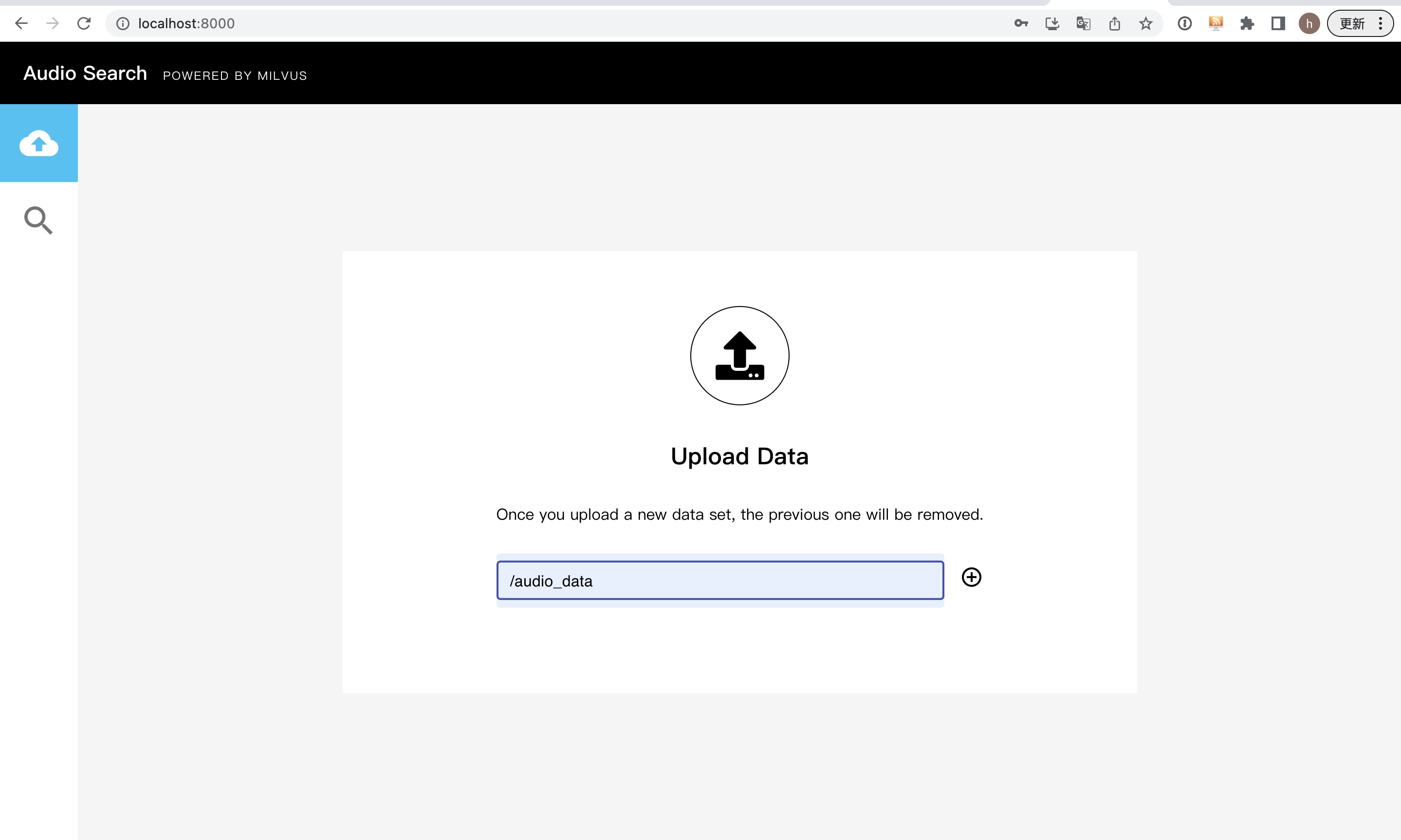
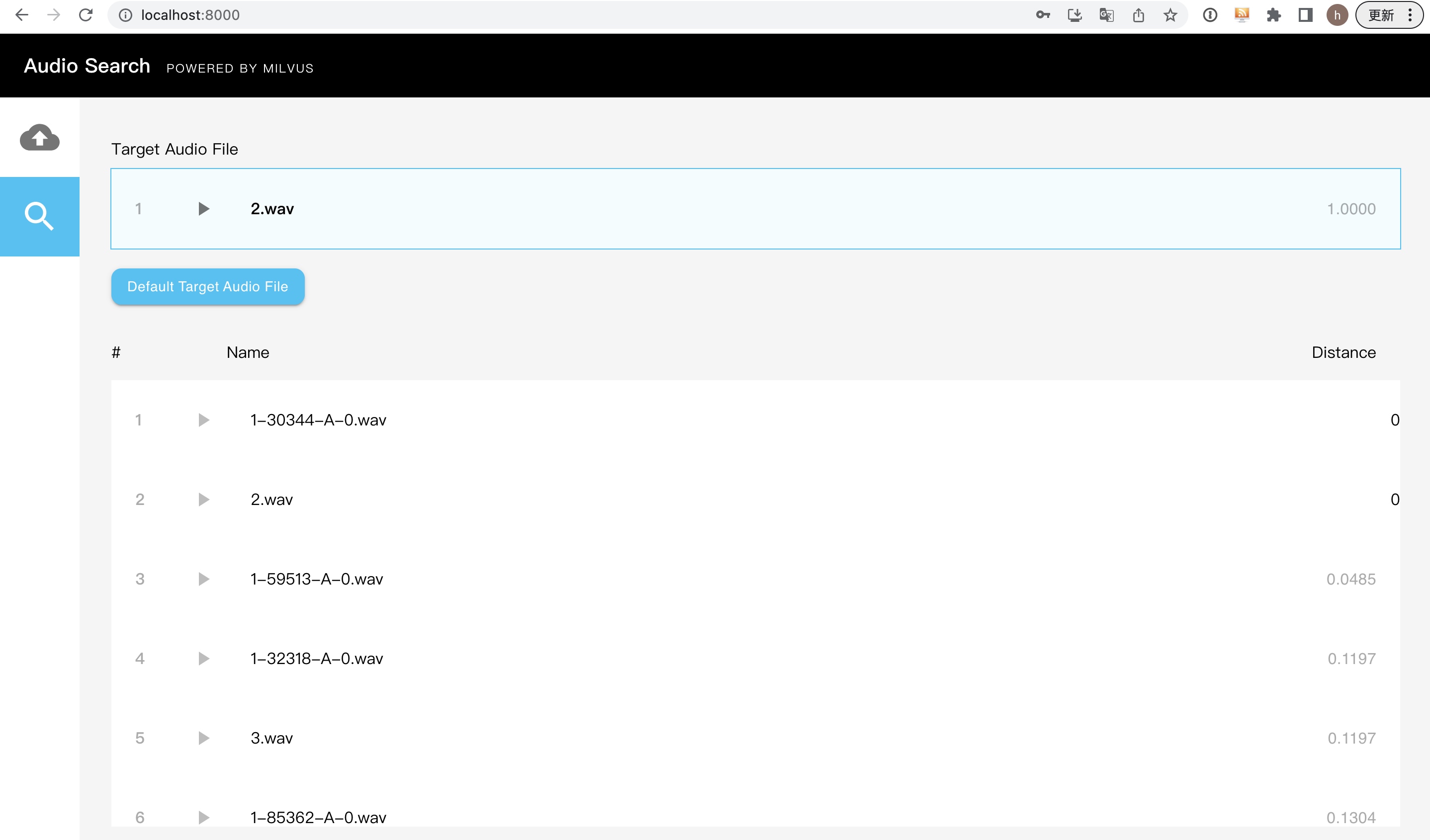
音频文件提取向量特征

提取音频文件的向量特征是语音处理中的一个重要任务。以下是一些常用的技术：

  1. MFCC（Mel频率倒谱系数）：MFCC 是一种常见的音频特征提取方法，它模拟了人耳的感知方式。它首先将音频信号转换为频谱图，然后将频率轴上的频率划分为若干个 Mel 频率带，最后计算每个频率带的功率谱，并将其转换为倒谱系数。MFCC 能够捕捉音频信号的频率和时域信息，常用于语音识别和语音合成等任务。

  2. 短时傅里叶变换（STFT）：STFT 是另一种常见的音频特征提取方法，它将音频信号分成若干个短时窗口，并对每个窗口进行傅里叶变换。这样可以得到每个窗口的频谱信息，从而捕捉音频信号的频率和时域信息。STFT 通常用于音频信号处理和音乐信息检索等任务。

  3. CQT（离散余弦变换）：CQT 是一种类似于 STFT 的方法，它使用一组不同的频率带宽来捕捉音频信号的频率信息。与 STFT 不同，CQT 可以在频率轴上对数刻度，这使得它能够更好地处理低频信号。CQT 通常用于音乐信息检索和音频分类等任务。

MFCC

MFCC（Mel-frequency cepstral coefficients）是一种常用的音频信号处理技术，用于提取音频的特征向量。其主要步骤如下：

  1. 预加重：对音频信号进行高通滤波，以增强高频部分的能量，减少低频部分的能量损失。

  2. 分帧：将音频信号分成若干帧，通常每帧的长度为20~40毫秒，相邻帧之间有重叠。

  3. 加窗：对每帧信号进行加窗处理，以减少帧边缘的突变，常用的窗函数有汉宁窗、汉明窗等。

  4. 傅里叶变换：对每帧信号进行快速傅里叶变换（FFT），得到每帧的频谱。

  5. 梅尔滤波器组：将频谱映射到梅尔频率上，梅尔频率是一种人耳感知的频率，梅尔滤波器组通常由20~40个滤波器组成，每个滤波器的带宽和中心频率不同。

  6. 取对数：对每个滤波器的输出取对数，得到每帧信号的梅尔频率倒谱系数（Mel-frequency cepstral coefficients，MFCC）。

  7. DCT变换：对每帧MFCC系数进行离散余弦变换（DCT），得到每帧的MFCC特征向量。

SFTF

STFT（Short-time Fourier transform）是一种常用的音频信号处理技术，用于将音频信号从时域（time domain）转换到频域（frequency domain）。其主要步骤如下：

  1. 将音频信号分成多个短时窗口，每个窗口长度为 N 个采样点，通常使用汉宁窗（Hanning window）等窗函数进行加窗处理，以减少频谱泄漏（spectral leakage）。

  2. 对于每个窗口，进行傅里叶变换（Fourier transform）得到其频谱（spectrum），即将时域信号转换为频域信号。可以使用快速傅里叶变换（Fast Fourier Transform，FFT）算法加速计算。

  3. 对于每个窗口的频谱，可以使用一些技术进行后处理，如使用对数幅度谱（logarithmic amplitude spectrum）代替线性幅度谱（linear amplitude spectrum），以更好地模拟人耳对声音的感知。

  4. 将所有窗口的频谱拼接起来，得到整个音频信号的频谱表示。这个频谱通常是一个二维矩阵，其中每一行表示一个频率，每一列表示一个时间窗口。

CQT

CQT（Constant-Q transform）是一种将音频信号从时域（time domain）转换到频域（frequency domain）的技术，其主要步骤如下：

  1. 将音频信号分成多个短时段，每个时段的长度通常为20~40毫秒。

  2. 对每个时段的信号进行加窗处理，以避免频谱泄露（spectral leakage）的问题。

  3. 对加窗后的信号进行傅里叶变换（Fourier transform）得到频域信号。

  4. 对频域信号进行滤波，以提取感兴趣的频率范围。

  5. 对滤波后的频域信号进行下采样（downsampling），以减少计算量。

  6. 重复上述步骤，直到处理完整个音频信号，得到音频的频谱表示。

python 代码实现

mfcc

import librosa
import numpy as np

# 加载音频文件
audio_file = '/data/2.wav'
y, sr = librosa.load(audio_file)

# 计算 MFCC 特征
mfccs = librosa.feature.mfcc(y=y, sr=sr, n_mfcc=13)

# 将 MFCC 特征转换为一维向量
mfccs_vector = np.mean(mfccs.T, axis=0)

print(mfccs_vector)

输出结果

[-3.7972183e+02  1.0088512e+02 -3.5129642e+00 -1.9051785e+01
 -2.3919962e+01 -2.5029432e+01 -1.4385112e+01 -1.0009483e+01
 -1.8019070e+01  2.9479107e-01  3.8208574e-02 -5.6408200e+00
 -2.3487382e+00]

stft

import librosa
import numpy as np

# 加载音频文件
audio_file = '/data/2.wav'
y, sr = librosa.load(audio_file)

# 计算 STFT 特征
stft = np.abs(librosa.stft(y))

# 将 STFT 特征转换为一维向量
stft_vector = np.mean(stft.T, axis=0)
print(stft_vector)


[6.4813397e-03 8.3055627e-03 1.2067630e-02 ... 3.4121547e-07 3.3004611e-07
 3.2894093e-07]

panns-inference

PANNs Inference 模型使用的是 STFT（短时傅里叶变换）来生成音频的特征向量。与 MFCC 和 CQT 相比，STFT 在音频信号处理中更常用，因为它能够提供更详细的频率和时间信息。

def get_audio_embedding(path):
    # Use panns_inference model to generate feature vector of audio
    try:
        RESAMPLE_RATE=32000
        audio, _ = librosa.core.load(path, sr=RESAMPLE_RATE, mono=True)
        if audio.size < RESAMPLE_RATE:
            audio = np.pad(audio, (0, RESAMPLE_RATE-audio.size), 'constant', constant_values=(0, 0))
        audio = audio[None, :]
        at = AudioTagging(checkpoint_path=None, device='cuda')
        _, embedding = at.inference(audio)
        embedding = embedding/np.linalg.norm(embedding)
        embedding = embedding.tolist()[0]
        return embedding
    except Exception as e:
        print(f"Error with embedding:{e}")
        return None

Cnn14_mAP=0.431.pth 是 PANNs Inference 模型的预训练权重文件，用于加载训练好的神经网络模型参数。这个模型是在音频分类任务上进行训练的，可以识别出不同的音频类别，比如说乐器、声音效果、人声等等。它是基于卷积神经网络 (CNN) 的架构，使用了 STFT 特征提取方法，输入的音频信号经过一系列卷积、池化、归一化等操作后，最终输出一个包含各个音频类别概率的向量。在使用 PANNs Inference 模型进行音频分类时，我们可以使用这个预训练权重文件来加载模型参数，从而进行预测。

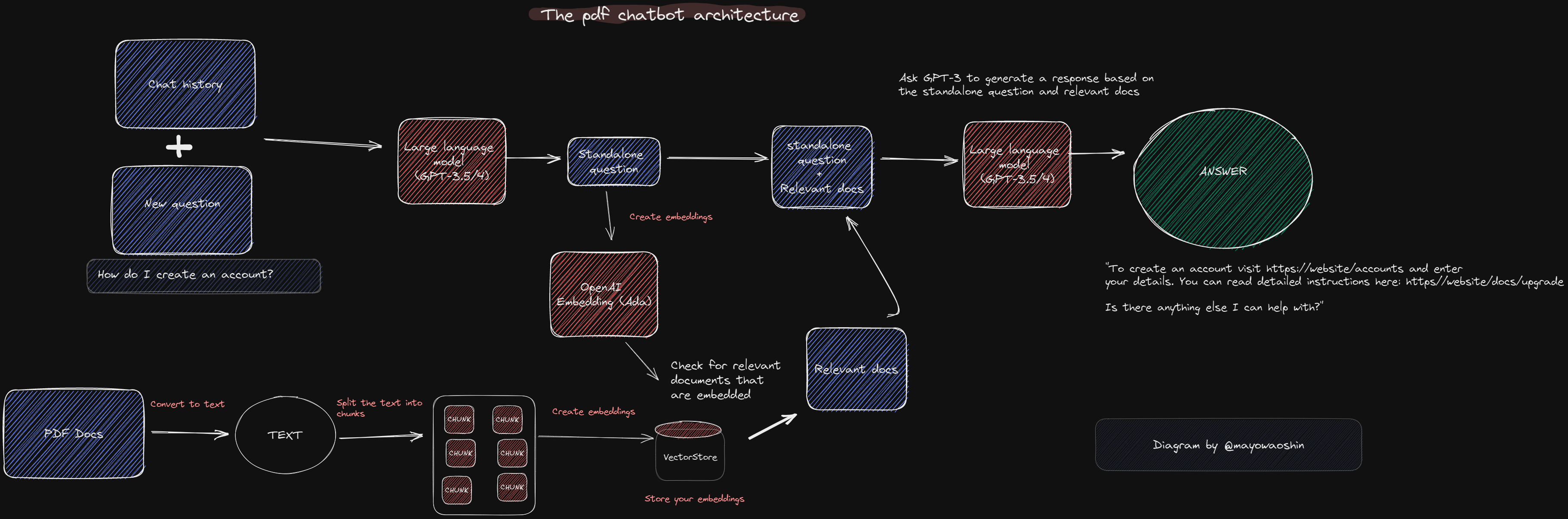
Chat With Your Docs

https://github.com/mayooear/gpt4-pdf-chatbot-langchain
gpt-langchain-pdf

https://wallstreetcn.com/articles/3688270
https://wallstreetcn.com/articles/3688423

https://www.youtube.com/watch?v=dN0lsF2cvm4
https://www.youtube.com/watch?v=u03AZlmZF_8

https://www.bilibili.com/video/BV1414y1c78514y1c785

2023/05/25 14:18 下午 posted in  AI

Copyright © 2015 Powered by MWeb,  Theme used GitHub CSS.